前情提要
在之前的视频中，我们讲到了动画是怎样构成的，其中最重要的一个函数就是 interpolate，能够对两个状态进行补间运算，运算式是这样写的
def interpolate (start, end, alpha):
return ( 1 - alpha) * start + alpha * end
def interpolate (start, end, alpha):
return ( 1 - alpha) * start + alpha * end
穿插一阶贝塞尔动画
其实在此处 interpolate 的含义变成了相对狭义的补间，即线性插值 . 但对三个值，甚至更多的值进行插值，也能够算作是补间. 因此，在这里我们采用 unity 中的一个函数 lerp，即线性插值函数，用于相互区分.
## 这里的算式和上面其实是一样的，而且我还是更喜欢上面的一种写法
def lerp (p0, p1, t):
return p0 + (p1 - p0) * t
## 这里的算式和上面其实是一样的，而且我还是更喜欢上面的一种写法
def lerp (p0, p1, t):
return p0 + (p1 - p0) * t
而对于 3 个值 P 0 , P 1 , P 2 \displaystyle{ P _{ 0 } , P _{ 1 } , P _{ 2 } } P 0 , P 1 , P 2
首先，我们应该很容易想到，先对某一部分，即 P 0 \displaystyle{ P _{ 0 } } P 0 P 1 \displaystyle{ P _{ 1 } } P 1 P 1 \displaystyle{ P _{ 1 } } P 1 P 2 \displaystyle{ P _{ 2 } } P 2 A , B \displaystyle{ A , B } A , B
A = lerp ( P 0 , P 1 , t ) B = lerp ( P 1 , P 2 , t ) \begin{aligned}
A&=\text{lerp}(P_0,P_1,t)\\
B&=\text{lerp}(P_1,P_2,t)
\end{aligned} A B = lerp ( P 0 , P 1 , t ) = lerp ( P 1 , P 2 , t )
穿插两个一阶贝塞尔动画
接着，我们再对 A \displaystyle{ A } A B \displaystyle{ B } B R \displaystyle{ R } R
R ( t ) = ( 1 − t ) ⋅ A + t ⋅ B = ( 1 − t ) [ ( 1 − t ) P 0 + t P 1 ] + t [ ( 1 − t ) P 1 + t P 2 ] = P 0 ( 1 − t ) 2 + 2 P 1 ( 1 − t ) t + P 2 t 2 \begin{aligned}
R(t)&=(1-t)\cdot A + t\cdot B\\
&=(1-t)[(1-t)P_0+tP_1]+t[(1-t)P_1+tP_2]\\
&=P_0(1-t)^2+2P_1(1-t)t+P_2t^2
\end{aligned} R ( t ) = ( 1 − t ) ⋅ A + t ⋅ B = ( 1 − t ) [( 1 − t ) P 0 + t P 1 ] + t [( 1 − t ) P 1 + t P 2 ] = P 0 ( 1 − t ) 2 + 2 P 1 ( 1 − t ) t + P 2 t 2 用代码来书写可以写成这样
def quadratic (p0, p1, p2, t):
A = lerp(p0, p1, t)
B = lerp(p1, p2, t)
return lerp(A, B, t)
def quadratic (p0, p1, p2, t):
A = lerp(p0, p1, t)
B = lerp(p1, p2, t)
return lerp(A, B, t)
而这其实就是贝塞尔曲线的方程了，这里的方程是二阶的，如果需要用三阶可以继续写下去.
穿插由二阶构造三阶的动画
def cubic (p0, p1, p2, p3, t):
A = quadratic(p0, p1, p2, t)
B = quadratic(p1, p2, p3, t)
return lerp(A, B, t)
def cubic (p0, p1, p2, p3, t):
A = quadratic(p0, p1, p2, t)
B = quadratic(p1, p2, p3, t)
return lerp(A, B, t)
经过归纳，我们可以得到 n \displaystyle{ n } n
B n ( t ) = ∑ i = 0 n P i ( n i ) ( 1 − t ) n − i t i , ( n i ) = n ! i ! ( n − i ) ! B^n(t)=\sum_{i=0}^{n}P_i{n\choose i}(1-t)^{n-i}t^i, {n\choose i}={n!\over i!(n-i)!} B n ( t ) = i = 0 ∑ n P i ( i n ) ( 1 − t ) n − i t i , ( i n ) = i ! ( n − i )! n ! 从贝塞尔曲线到概率模型
我知道这一部分很扯，但不知道为什么我就是能想到这一步
n \displaystyle{ n } n
B 3 ( t ) = ( 3 0 ) P 0 ( 1 − t ) 3 + ( 3 1 ) P 1 ( 1 − t ) 2 t + ( 3 2 ) P 2 ( 1 − t ) t 2 + ( 3 3 ) P 3 t 3 = P 0 ( 1 − t ) 3 + 3 P 1 ( 1 − t ) 2 t + 3 P 2 ( 1 − t ) t 2 + P 3 t 3 = P 0 ( − t 3 + 3 t 2 − 3 t + 1 ) + P 1 ( 3 t 3 − 6 t 2 + 3 t ) + P 2 ( 3 t 2 − 3 t 3 ) + P 3 t 3 \begin{aligned}
B^3(t)=&{3\choose 0}P_0(1-t)^3+{3\choose 1}P_1(1-t)^2t+{3\choose 2}P_2(1-t)t^2+{3\choose 3}P_3t^3\\
=&P_0(1-t)^3+3P_1(1-t)^2t+3P_2(1-t)t^2+P_3t^3\\
=&P_0(-t^3+3t^2-3t+1)\\
+&P_1(3t^3-6t^2+3t)\\
+&P_2(3t^2-3t^3)\\
+&P_3t^3
\end{aligned} B 3 ( t ) = = = + + + ( 0 3 ) P 0 ( 1 − t ) 3 + ( 1 3 ) P 1 ( 1 − t ) 2 t + ( 2 3 ) P 2 ( 1 − t ) t 2 + ( 3 3 ) P 3 t 3 P 0 ( 1 − t ) 3 + 3 P 1 ( 1 − t ) 2 t + 3 P 2 ( 1 − t ) t 2 + P 3 t 3 P 0 ( − t 3 + 3 t 2 − 3 t + 1 ) P 1 ( 3 t 3 − 6 t 2 + 3 t ) P 2 ( 3 t 2 − 3 t 3 ) P 3 t 3 可以发现，在最后一步把立方、平方等项拆开的时候，这些式子的和很像是一个加权平均数，或者说是一个数学期望. 而更巧合的事情发生了，我们分别设 P i \displaystyle{ P _{ i } } P i a i ( i = 0 , 1 , 2 , 3 ) \displaystyle{ a _{ i } \left( i = 0 , 1 , 2 , 3 \right) } a i ( i = 0 , 1 , 2 , 3 )
a 0 + a 1 + a 2 + a 3 = ( − t 3 + 3 t 2 − 3 t + 1 ) + ( 3 t 3 − 6 t 2 + 3 t ) + ( 3 t 2 − 3 t 3 ) + t 3 = 1 \displaystyle{ a _{ 0 } + a _{ 1 } + a _{ 2 } + a _{ 3 } = \left( - t ^{ 3 } + 3 t ^{ 2 } - 3 t + 1 \right) + \left( 3 t ^{ 3 } - 6 t ^{ 2 } + 3 t \right) + \left( 3 t ^{ 2 } - 3 t ^{ 3 } \right) + t ^{ 3 } = 1 } a 0 + a 1 + a 2 + a 3 = ( − t 3 + 3 t 2 − 3 t + 1 ) + ( 3 t 3 − 6 t 2 + 3 t ) + ( 3 t 2 − 3 t 3 ) + t 3 = 1 也就是说，a i ( i = 0 , 1 , 2 , 3 ) \displaystyle{ a _{ i } \left( i = 0 , 1 , 2 , 3 \right) } a i ( i = 0 , 1 , 2 , 3 ) P i ( i = 0 , 1 , 2 , 3 ) \displaystyle{ P _{ i } \left( i = 0 , 1 , 2 , 3 \right) } P i ( i = 0 , 1 , 2 , 3 ) B 3 ( t ) \displaystyle{ B ^{ 3 } \left( t \right) } B 3 ( t )
这么说着抽象的事件似乎会让人摸不着头脑，我们不妨把 P i \displaystyle{ P _{ i } } P i B 3 ( t ) \displaystyle{ B ^{ 3 } \left( t \right) } B 3 ( t ) P i ( i = 0 , 1 , 2 , 3 ) \displaystyle{ P _{ i } \left( i = 0 , 1 , 2 , 3 \right) } P i ( i = 0 , 1 , 2 , 3 ) 这个期望似乎 会随着 t \displaystyle{ t } t
我们尝试写出这个分布列（随机变量 X \displaystyle{ X } X P 0 , P 1 , P 2 , P 3 \displaystyle{ P _{ 0 } , P _{ 1 } , P _{ 2 } , P _{ 3 } } P 0 , P 1 , P 2 , P 3
X \displaystyle{ X } X P 0 \displaystyle{ P _{ 0 } } P 0 P 1 \displaystyle{ P _{ 1 } } P 1 P 2 \displaystyle{ P _{ 2 } } P 2 P 3 \displaystyle{ P _{ 3 } } P 3 p \displaystyle{ p } p ( 1 − t ) 3 \displaystyle{ \left( 1 - t \right) ^{ 3 } } ( 1 − t ) 3 3 ( 1 − t ) 2 t \displaystyle{ 3 \left( 1 - t \right) ^{ 2 } t } 3 ( 1 − t ) 2 t 3 ( 1 − t ) t 2 \displaystyle{ 3 \left( 1 - t \right) t ^{ 2 } } 3 ( 1 − t ) t 2 t 3 \displaystyle{ t ^{ 3 } } t 3
对于 t \displaystyle{ t } t [ 0 , 1 ] \displaystyle{ \left[ 0 , 1 \right] } [ 0 , 1 ]
但我们反过来思考一下，如果是一个随机变量 Y ′ \displaystyle{ Y ^{\prime} } Y ′ Y ′ ∼ ( 0 1 q p ) Y'\sim \left(\begin{array}{l} 0 & 1 \\ q & p\end{array} \right) Y ′ ∼ ( 0 q 1 p ) n \displaystyle{ n } n Y ∼ B ( n , p ) Y\sim B(n,p) Y ∼ B ( n , p )
P ( Y = m ) = ( n m ) ( 1 − t ) n − m t m ( 0 ⩽ m ⩽ n , m ∈ N ) P(Y=m)={n\choose m}(1-t)^{n-m}t^m\qquad(0\leqslant m \leqslant n,m\in\mathbb{N}) P ( Y = m ) = ( m n ) ( 1 − t ) n − m t m ( 0 ⩽ m ⩽ n , m ∈ N ) 这是一个二项分布，而概率似乎与贝塞尔曲线方程的某些系数一模一样. 同时，这两者也有一些共通性. 在贝塞尔曲线中，t \displaystyle{ t } t [ 0 , 1 ] \displaystyle{ \left[ 0 , 1 \right] } [ 0 , 1 ] [ 0 , 1 ] \displaystyle{ \left[ 0 , 1 \right] } [ 0 , 1 ]
建立二项分布模型 增大样本容量
某人射击打靶，射中的概率为 p \displaystyle{ p } p n \displaystyle{ n } n m \displaystyle{ m } m n \displaystyle{ n } n X \displaystyle{ X } X X \displaystyle{ X } X X ∼ B ( n , p ) X\sim B(n,p) X ∼ B ( n , p )
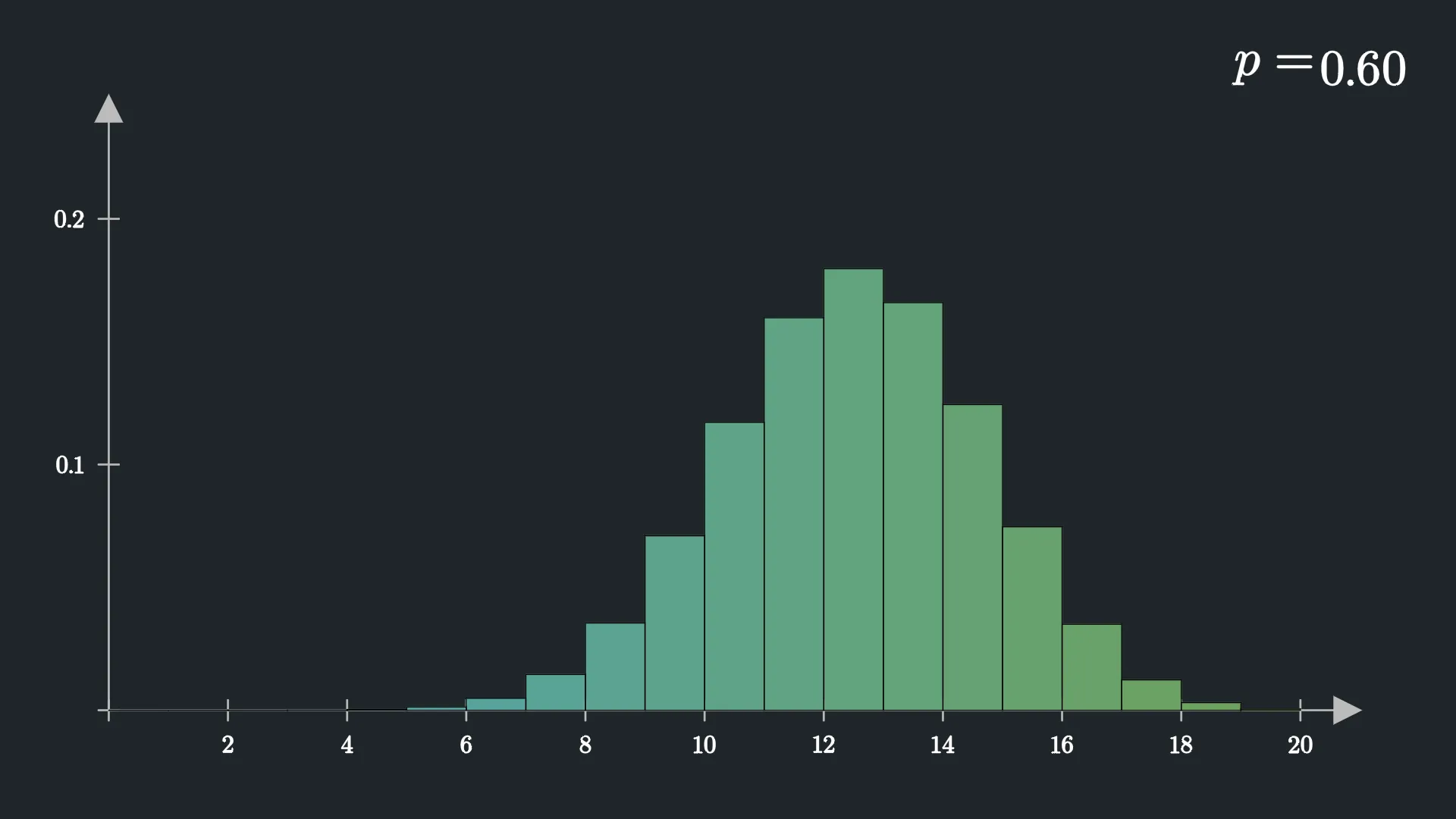
现在还没有代入具体数字，我们似乎没法给出一些明确的答案. 那么我们不妨就让 n = 20 , p = 0.6 \displaystyle{ n = 20 , p = 0.6 } n = 20 , p = 0.6 m \displaystyle{ m } m
P ( X = m ) = ( n m ) ( 1 − p ) n − m p m = ( 20 m ) ( 2 5 ) 20 − m ( 3 5 ) m \begin{aligned}
P(X=m)&={n\choose m}(1-p)^{n-m}p^m\\
&={20\choose m}\left({2\over 5}\right)^{20-m}\left({3\over 5}\right)^m
\end{aligned} P ( X = m ) = ( m n ) ( 1 − p ) n − m p m = ( m 20 ) ( 5 2 ) 20 − m ( 5 3 ) m 同时，我们用图像画出每个 m \displaystyle{ m } m X \displaystyle{ X } X m \displaystyle{ m } m
可以看到，整个图像呈现出中间高，两边低的样子.
（概率论经典题）有时我们可能会遇到这样的问题，假设击中次数为 m \displaystyle{ m } m P ( m 1 ⩽ m < m 2 ) P(m_1\leqslant m < m_2) P ( m 1 ⩽ m < m 2 ) m \displaystyle{ m } m
P ( m 1 ⩽ m < m 2 ) = ∑ m = m 1 m 2 − 1 P ( X = m ) P(m_1\leqslant m<m_2)=\displaystyle\sum_{m=m_1}^{m_2-1}P(X=m) P ( m 1 ⩽ m < m 2 ) = m = m 1 ∑ m 2 − 1 P ( X = m ) 也就是只需要将图中在范围内的矩形面积相加就可以了. 同样地，所有这些事件的概率之和为 1 \displaystyle{ 1 } 1
P ( 0 ⩽ m ⩽ n ) = ∑ m = 0 n P ( X = m ) = 1 P(0\leqslant m\leqslant n)=\displaystyle\sum_{m=0}^{n}P(X=m)=1 P ( 0 ⩽ m ⩽ n ) = m = 0 ∑ n P ( X = m ) = 1 在这里，矩形数量并不多，如果所需要计算的量比较少，那么就可以直接手算计算机运算相加就可以了.
但如果样本很多，范围也很大呢？这样用手算一个一个相加肯定是相当耗费精力的.
进一步增大样本容量
现在，我们将试验次数增加. 之前提到了用面积来表示 X = m \displaystyle{ X = m } X = m
这时我们发现，我们需要不断地拉长横轴，不妨给横轴除以 n \displaystyle{ n } n n \displaystyle{ n } n X = m \displaystyle{ X = m } X = m n P ( X = m ) \displaystyle{ n P \left( X = m \right) } n P ( X = m ) m \displaystyle{ m } m m n {m\over n} n m
现在，横轴所表示的变量取值范围变成了 [ 0 , 1 ] \displaystyle{ \left[ 0 , 1 \right] } [ 0 , 1 ] p \displaystyle{ p } p p \displaystyle{ p } p [ 0 , 1 ] \displaystyle{ \left[ 0 , 1 \right] } [ 0 , 1 ] 近似 的看作是连续的. 也就是说，当二项分布的样本容量足够大时，它的概率分布可以近似地看作是一个连续型的分布.
原本打算在这里插入如何从二项分布推导正态分布，但是难度还是有一点的。然而，写到这里发现讨论的方向似乎错了，原因如下
到这里为止，这个“贝塞尔曲线的平滑”与“近似连续型的分布”本质上还有很大的区别，前者指的是通过一个 B n ( t ) \displaystyle{ B ^{ n } \left( t \right) } B n ( t ) n \displaystyle{ n } n t \displaystyle{ t } t n \displaystyle{ n } n 所以讨论到这里，方向好像偏掉了
