反向传播算法
- 输入层 x=(x1,…,xd)
- 隐藏层 b=(b1,…,bq)
- 输出层 y^=(y1,…,yl)
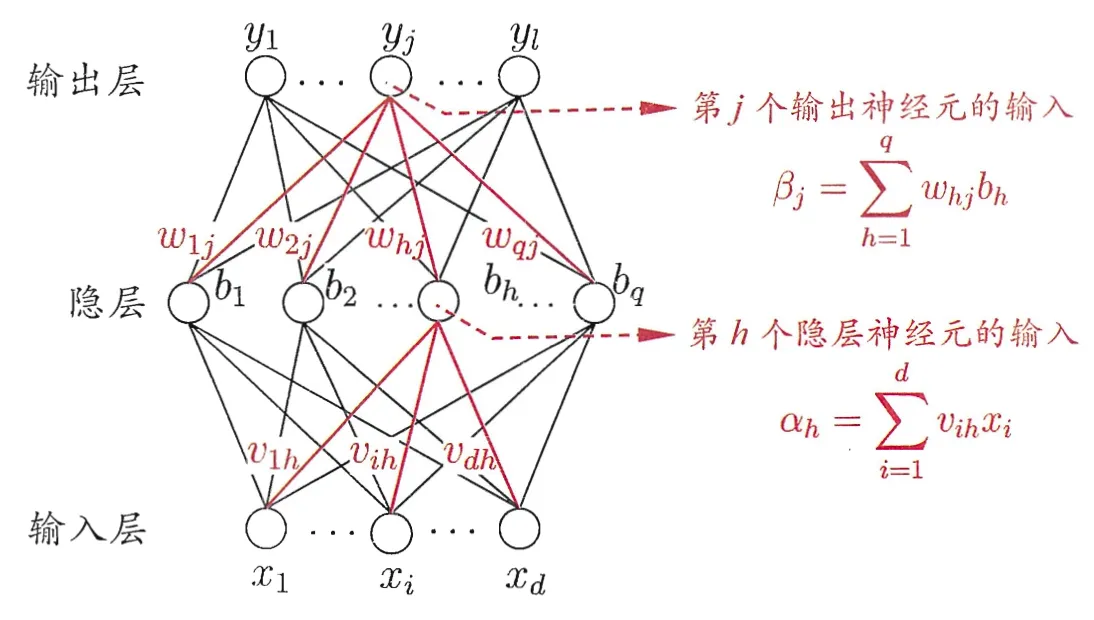
训练数据 (xk,yk),神经网络输出 y^k=(y^1k,…,y^lk)
y^j=f(βj−θj)
为了求导方便,设定均方误差 Ek=21j=1∑l(y^jk−yjk)2,前面有一个 21
参数调整的量为 Δwhj=−η∂whj∂Ek,η 是学习率,是人提供的,那么就要推导右侧的部分
βj=h=1∑qwhjbh
∂whj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj=(y^jk−yjk)⋅(???)⋅bh=(y^jk−yjk)⋅y^jk(1−y^jk)⋅bh
f 为 sigmoid 函数,可以求出其导数 f′=f(1−f)

