Skip to content
Notes

第 8 章 密码协议

8.1. 一些基本协议

8.1.3. 数字承诺协议

数字承诺协议是指发送方暂时以隐藏的方式向接收方承诺一个值，承诺后不能再对该值做出任何修改。

数字承诺协议通常有两步组成：

  1. 承诺，发送方将一个消息锁进一盒中，再将该盒发送给接收方
  2. 展示，发送方打开盒，以向接收方展示盒中内容

数字承诺协议必须满足以下两个性质：

  • 隐藏性：第一步完成后，接收者无法获得发送者所承诺的值。如果接收者是概率多项式时间的，则称方案是计算上隐藏的。如果接收者有无穷的计算能力，则称方案是完备隐藏的。
  • 捆绑性：上述第二步完成后，发送者只能向接收者展示一个值。类似于隐藏性，捆绑性也分为计算上的和完备的。

1. 基于二次剩余的数字承诺

公开参数
  • n\displaystyle{ n } 是两个大素数 p,q\displaystyle{ p , q } 的乘积，即 n=pq\displaystyle{ n = p q }
  • x∈Zn∗,(xn)=1x \in \mathbb{Z}_n^\ast, \left({x \over n} \right)=1，x\displaystyle{ x } 是模 n\displaystyle{ n } 的非二次剩余
步骤
  1. 发送者随机选 r←RZn∗r \leftarrow {}_R\mathbb{Z}^\ast _n，计算 c≡r2xb(modn)c \equiv r^2 x^b \pmod n，作为对 b∈{0,1}b \in \{0, 1\} 的承诺
  2. 为了展示承诺，发送者将 (b,r)\displaystyle{ \left( b , r \right) } 发送给接收者，接收者验证 r2xb(modn)≡cr^2 x^b \pmod n \equiv c 是否成立。如果成立，则接受。
性质
  • 隐藏性：接收者若能从 c\displaystyle{ c } 中得出 b=0\displaystyle{ b = 0 }，则可知 c\displaystyle{ c } 是二次剩余；若能得出 b=1\displaystyle{ b = 1 }，则可知 c\displaystyle{ c } 是非二次剩余。与判断 c\displaystyle{ c } 是二次剩余还是非二次剩余的困难性矛盾。因此，方案是完备隐藏的。
  • 捆绑性：如果发送者能将某一 c\displaystyle{ c } 打开到两组不同值 (b1,r1)≠(b2,r2)(b_1, r_1) \ne (b_2, r_2)，必有 b1≠b2,r1≠r2b_1 \ne b_2, r_1 \ne r_2。因此 r12xb1≡r22xb2 mod nr_1^2 x^{b_1} \equiv r_2^2 x^{b_2} \bmod n，(r1r2)2≡xb2−b1≡x(or x−1) mod n\left( {r_1 \over r_2} \right)^2 \equiv x ^{b_2 - b_1} \equiv x (\text{or } x^{-1}) \bmod n，与 x\displaystyle{ x } 是非二次剩余矛盾。

2. Pedersen 数字承诺

Pedersen 数字承诺协议是基于离散对数困难性假设的。

参数
  • p,q\displaystyle{ p , q } 是两个大素数，q∣p−1q \mid p-1
  • Gq\mathbb{G}_q 是 Zp∗\mathbb{Z}_p^\ast 的阶为 q\displaystyle{ q } 的子群
  • g,h\displaystyle{ g , h } 是 Gq\mathbb{G}_q 的生成元，但收发双方都不知道 log⁡g(h)\log_g(h)
步骤
  1. 发送者为做对 x∈Zqx \in \mathbb{Z}_q 的承诺，随机选择 r←RZqr \leftarrow {}_R \mathbb{Z}_q，计算 c≡gxhr mod pc \equiv g^x h^r \bmod p 并发送给接收者
  2. 为了展示承诺，发送者将 (x,r)\displaystyle{ \left( x , r \right) } 发送给接收者，接收者验证 gxhr mod p≡cg^x h^r \bmod p \equiv c 是否成立。如果成立，则接受。
性质
  • 隐藏性：已知承诺 c\displaystyle{ c }，每个 x′∈Zqx^\prime \in \mathbb{Z}_q 都可能是所承诺的值。即如果 c≡gxhr mod pc \equiv g^x h^r \bmod p，对任一 x′∈Zqx^\prime \in \mathbb{Z}_q，由 gxhr≡gx′hr′ mod pg^x h^r \equiv g^{x^\prime} h^{r^\prime} \bmod p，得 gx−x′≡hr′−r mod pg^{x - x^\prime} \equiv h^{r^\prime - r} \bmod p，x−x′≡(r′−r)log⁡g(h) mod qx - x^\prime \equiv (r^\prime - r) \log_g(h) \bmod q，r′≡r+x−x′log⁡g(h)(modq)r^\prime \equiv r + {x - x ^\prime \over \log_g(h) } \pmod{q}，即存在 r′r^\prime （虽然不知道 log⁡g(h)\log_g(h) 而不能计算），满足 c≡gx′hr′ mod pc \equiv g^{x^\prime} h^{r^\prime} \bmod p，即 x′x^\prime 也是 c\displaystyle{ c } 所承诺的值。所以由 c\displaystyle{ c } 不能确定是对哪个 x∈Zqx \in \mathbb{Z}_q 的承诺。
  • 捆绑性：如果发送者能对两组不同的 (x,r),(x′,r′)(x,r),(x^\prime, r^\prime) 承诺到同一值，则由 gxhr≡gx′hr′ mod pg^x h^r \equiv g^{x^\prime} h^{r^\prime} \bmod p，得 log⁡g(h)≡x−x′r′−r mod q\log_g(h) \equiv {x - x^\prime \over r^\prime - r } \bmod q，即发送者能计算 log⁡g(h)\log_g(h)，矛盾。

8.1.4. 不经意传输协议

设 A 有一个秘密，想以 1/2 的概率传递给 B ，即 B 有 50% 的机会收到这个秘密，另外 50% 的机会什么也没有收到，协议执行完后，B 知道自己是否收到了这个秘密，但 A 却不知 B 是否收到了这个秘密。这种协议就称为不经意传输协议。

1. 基于大数分解问题的不经意传输协议

设 A 想通过不经意传输协议传递给 B 的秘密是整数 n\displaystyle{ n } (为两个大素数之积)的因数分解。这个问题具有普遍意义，因为任何秘密都可通过 RSA 加密，得到 n\displaystyle{ n } 的因数分解就可得到这个秘密。

协议基于如下事实：已知某数在模 n\displaystyle{ n } 下两个不同的平方根，就可分解 n\displaystyle{ n }。

  1. B 随机选一数 x\displaystyle{ x }，将 x2 mod nx^2 \bmod n 发送给 A
  2. A (掌握 n=pq\displaystyle{ n = p q } 的分解) 计算 x2 mod nx^2 \bmod n 的四个平方根 ±x,±y\pm x, \pm y ，并将其中之一发送给 B 。由于 A 只知道 x2 mod nx^2 \bmod n ，并不知道四个平方根中哪一个是 B 选的 x\displaystyle{ x }
  3. B 检查第二步收到的数是否与 ±x\pm x 在模 n\displaystyle{ n } 下同余，如果是，则 B 没有得到任何新信息;否则 B 就掌握了 x2 mod nx^2 \bmod n 的两个不同的平方根，从而能够分解 n\displaystyle{ n }。而 A 却不知究竟是哪种情况

显然，B 得到 n\displaystyle{ n } 的分解的概率为 12\displaystyle{ \frac{ 1 }{ 2 } }

8.2. 零知识证明

它指的是证明者能够在不向验证者提供任何有用的信息的情况下，使验证者相信某个论断是正确的

零知识证明实质上是一种涉及两方或更多方的协议，即两方或更多方完成一项任务所需采取的一系列步骤。证明者向验证者证明并使其相信自己知道或拥有某一消息，但证明过程不能向验证者泄漏任何关于被证明消息的信息。

例子

A 要向 B 证明自己拥有某个房间的钥匙，假设该房间只能用钥匙打开锁，而其他任何方法都打不开。这时有 2 个方法

  • A 把钥匙出示给 B，B 用这把钥匙打开该房间的锁，从而证明 A 拥有该房间的正确的钥匙。
  • B 确定该房间内有某一物体，A 用自己拥有的钥匙打开该房间的门，然后把物体拿出来出示给 B ，从而证明自己确实拥有该房间的钥匙。

第二种方法属于零知识证明。好处在于：在整个证明的过程中，B 始终不能看到钥匙的样子，从而避免了钥匙的泄露。

8.2.1. 交互证明系统

交互证明系统由两方参与，分别称为证明者 Prover 和验证者 Verifier ，其中 P\mathcal{P} 知道某一秘密，P\mathcal{P} 希望 V\mathcal{V} 相信自己的确掌握这一秘密。

交互证明由若干轮组成，在某一轮，P\mathcal{P} 和 V\mathcal{V} 可能需根据从对方收到的消息和自己计算的某个结果决定向对方发送的消息。比较经典的方式是在每轮 V\mathcal{V} 都向 P\mathcal{P} 发出一询问， P\mathcal{P} 向 V\mathcal{V} 做出一应答。所有轮执行完后， V\mathcal{V} 根据 P\mathcal{P} 是否在每一轮对自己发出的询问都能正确应答，以决定是否接受 P\mathcal{P} 的证明。

交互证明与数学证明的区别
  • 数学证明的证明者可自己独立地完成证明，相当于笔试
  • 交互证明是由 P\mathcal{P} 一步一步地产生证明、 V\mathcal{V} 一步一步地验证证明的有效性来实现，相当于口试，因此双方之间通过某种信道的通信是必需的。

交互证明系统需满足以下要求

  • 完备性:如果 P\mathcal{P} 知道某一秘密， V\mathcal{V} 将接受 P\mathcal{P}
  • 可靠性:如果 P\mathcal{P} 能以一定的概率使 V\mathcal{V} 相信的证明，则 P\mathcal{P} 知道相应的秘密。

例 证明者 P\mathcal{P} 有两个同构图 G,H\displaystyle{ G , H }，向验证者证明 G≅HG \cong H，即从 G\displaystyle{ G } 的顶点集到 H\displaystyle{ H } 的顶点集存在一个一一映射， P\mathcal{P} 只须向 V\mathcal{V} 出示这个映射。

样例
graph LR subgraph G e --- b --- a --- c --- d --- e b --- c end subgraph H x --- y --- z --- u --- v --- x y --- u end
%%{init: {'theme':'dark'}}%% graph LR subgraph G e --- b --- a --- c --- d --- e b --- c end subgraph H x --- y --- z --- u --- v --- x y --- u end
π={(x,e),(y,b),(z,a),(u,c),(v,d)}\pi=\{ (x,e), (y,b), (z,a), (u,c), (v,d) \}

8.2.3. 交互证明系统的零知识性

零知识证明起源于最小泄露证明。

在交互系统中，设 P\mathcal{P} 知道某一秘密，并向 V\mathcal{V} 证明自己掌握这一秘密，但又不向 V\mathcal{V} 泄露这一秘密，这就是最小泄露证明。

进一步，如果 V\mathcal{V} 除了知道 P\mathcal{P} 能证明某一事实外，不能得到其他任何信息，则称 P\mathcal{P} 实现了零知识证明，相应的协议称为零知识证明协议。

例 一个简单的迷宫，C D 之间有一道门，需要知道秘密口令才能将其打开。 P\mathcal{P} 向 V\mathcal{V} 证明自己能打开这道门，但又不愿意向 V\mathcal{V} 泄露秘密口令。

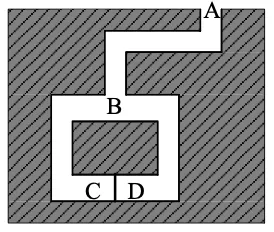
可采用的协议
  1. V\mathcal{V} 开始时停留在 A
  2. P\mathcal{P} 一直走到迷宫深处，随机选择位置 C 或 D
  3. P\mathcal{P} “消失”后， V\mathcal{V} 走到 B 处，命令 P\mathcal{P} 从某个出口返回 B
  4. P\mathcal{P} 服从 V\mathcal{V} 的命令，必要时利用秘密口令打开 C 与 D 之间的门
  5. 重复以上过程 n\displaystyle{ n } 次

协议中，如果 P\mathcal{P} 不知道秘密口令，就只能原路返回，不能呢个走另一条路。 P\mathcal{P} 每次猜对 V\mathcal{V} 要求走哪的概率是 12\displaystyle{ \frac{ 1 }{ 2 } }，因此每轮能欺骗的概率为 12\displaystyle{ \frac{ 1 }{ 2 } }。假定 n=16\displaystyle{ n = 16 }，则 P\mathcal{P} 欺骗 V\mathcal{V} 的概率为 12{16}\displaystyle{ \frac{ 1 }{ 2 ^{ \left\lbrace 16 \right\rbrace } } }。如果每次 P\mathcal{P} 都能按 V\mathcal{V} 的要求返回， V\mathcal{V} 即能证明 P\mathcal{P} 确实知道秘密口令。

同时 V\mathcal{V} 无法获取丝毫关于 P\mathcal{P} 秘密口令的信息，所以这是一个零知识证明。

8.2.4. 非交互式证明系统

在上述交互式证明系统中，如果 P\mathcal{P} 和 V\mathcal{V} 不进行交互，证明由 P\mathcal{P} 产生后直接给 V\mathcal{V} ， V\mathcal{V} 对证明直接进行验证，这种证明系统称为非交互式证明系统

Non-Interactive Zero-Knowledge

8.2.8. 知识证明

知识证明指证明者 P\mathcal{P} 向验证者 V\mathcal{V} 证明自己掌握一知识，但又不出示这个知识。例如 P\mathcal{P} 向 V\mathcal{V} 证明自己掌握一口令，但不向 V\mathcal{V} 出示这个口令。又如已知一公开钥 PK\displaystyle{ P K }， P\mathcal{P} 向 V\mathcal{V} 证明自己知道与 PK\displaystyle{ P K } 对应的秘密钥 SK\displaystyle{ S K }。

在知识的证明过程中，如果 P\mathcal{P} 没有再泄露其他额外的信息，则称该知识证明是零知识的

例 A\displaystyle{ A } 为公钥

已知循环群 G=⟨g⟩=⟨h⟩,A=gxhy\mathbb{G} =\langle g \rangle = \langle h \rangle, A=g^x h^y， P\mathcal{P} 向 V\mathcal{V} 证明知道 x,y\displaystyle{ x , y }

协议
  1. P\mathcal{P} 随机选取 r1,r2←RZqr_1,r_2 \leftarrow {}_R \mathbb{Z}_q，计算 t≡gr1hr2 mod qt \equiv g^{r_1} h^{r_2} \bmod q，将 t\displaystyle{ t } 发送给 V\mathcal{V}
  2. V\mathcal{V} 随机选 c←RZqc \leftarrow {}_R \mathbb{Z}_q，将 c\displaystyle{ c } 发送给 P\mathcal{P}
  3. P\mathcal{P} 计算 s1≡xc+r1(modq),s2≡yc+r2(modq)s_1 \equiv xc+r_1 \pmod q, s_2 \equiv yc+r_2 \pmod q，将 (s1,s2)\displaystyle{ \left( s _{ 1 } , s _{ 2 } \right) } 发送给 V\mathcal{V}
  4. V\mathcal{V} 检查 g{s1}h{s2}=Act\displaystyle{ g ^{ \left\lbrace s _{ 1 } \right\rbrace } h ^{ \left\lbrace s _{ 2 } \right\rbrace } = A ^{ c } t } 是否成立，成立则接受 P\mathcal{P} 的证明，否则拒绝
gs1hs2=gxc+r1hyc+r2=gxcgr1hychr2=(gxhy)cgr1hr2≡Act(modq)\begin{aligned} g^{s_1} h^{s_2} & = g^{xc + r_1} h^{yc + r_2} \\ & = g^{xc} g^{r_1} h^{yc} h^{r_2} \\ & = (g^x h^y)^c g^{r_1} h^{r_2} \\ & \equiv A^c t \pmod q \end{aligned}

例 PK{A=gα,B=hα}PK \{ A=g^\alpha , B=h^\alpha \}

已知循环群 G=⟨g⟩=⟨h⟩,A=gx,B=hx\mathbb{G} =\langle g \rangle = \langle h \rangle, A=g^x, B=h^x， P\mathcal{P} 向 V\mathcal{V} 证明知道 x\displaystyle{ x } 且 (g,h,A,B)\displaystyle{ \left( g , h , A , B \right) } 形成 DDH 元组（判定 Diffie-Hellman 问题）即 A,B\displaystyle{ A , B } 有相同指数 x\displaystyle{ x }

协议
  1. P\mathcal{P} 随机选 r←RZqr \leftarrow {}_R\mathbb{Z}_q，计算 t1≡gr mod q,t2≡hr mod qt_1 \equiv g^r \bmod q, t_2 \equiv h^r \bmod q，将 t1,t2\displaystyle{ t _{ 1 } , t _{ 2 } } 发送给 V\mathcal{V}
  2. V\mathcal{V} 随机选 c←RZqc \leftarrow {}_R\mathbb{Z}_q，将 c\displaystyle{ c } 发送给 P\mathcal{P}
  3. P\mathcal{P} 计算 s≡xc+r(modq)s \equiv xc+r \pmod q，将 s\displaystyle{ s } 发送给 V\mathcal{V}
  4. V\mathcal{V} 检查 gs=Act1,hs=Bct2\displaystyle{ g ^{ s } = A ^{ c } t _{ 1 } , h ^{ s } = B ^{ c } t _{ 2 } } 是否成立，若成立则接受 P\mathcal{P} 的证明

DDH 问题：给定四元组 g,gμ,gν,gκ∈Gg, g^\mu, g^\nu, g^\kappa \in \mathbb{G}，如果 κ=μν\kappa = \mu \nu，则输出真，否则输出假

协议证明了 P\mathcal{P} 知道 x\displaystyle{ x }，是否也证明了 (g,h,A,B)\displaystyle{ \left( g , h , A , B \right) } 形成 DDH 元组？

解答

若 A=gx,B=hx′,x≠x′A = g^x, B = h^{x ^\prime}, x \ne x^\prime， P\mathcal{P} 选择 r1,r2←RZq,r1≠r2r_1,r_2 \leftarrow {}_R \mathbb{Z}_q, r_1 \ne r_2

若 r1=r2\displaystyle{ r _{ 1 } = r _{ 2 } }，则由 gs=Act1\displaystyle{ g ^{ s } = A ^{ c } t _{ 1 } } 和 hs=Bct2\displaystyle{ h ^{ s } = B ^{ c } t _{ 2 } } 得 s≡xc+r1(modq),s≡x′c+r2(modq)s \equiv xc+r_1 \pmod q, s \equiv x^\prime c+r_2 \pmod q，与 x≠x′x \ne x^\prime 矛盾

计算 t1≡gr1 mod q,t2≡hr2 mod qt_1 \equiv g^{r_1} \bmod q, t_2 \equiv h^{r_2} \bmod q，协议其他部分保持不变。gs=Act1,hs=Bct2\displaystyle{ g ^{ s } = A ^{ c } t _{ 1 } , h ^{ s } = B ^{ c } t _{ 2 } } 成立，仅当 xc+r1≡x′c+r2(modq)xc+r_1 \equiv x^\prime c + r_2 \pmod q，即 c=r1−r2x′−x(modq)c = {r_1-r_2 \over x^\prime - x} \pmod q 时，验证方程成立。

而 V\mathcal{V} 选到这个特定值 c\displaystyle{ c } 的概率是可以忽略的，所以 P\mathcal{P} 欺骗成功的概率是可忽略的。