第 4 章 串

4.2. 串的模式匹配

4.2.1. 简单的模式匹配算法

function strMatch(s1: string, s2: string): number {
  let i = 0
  let j = 0
  while (i < s1.length && j < s2.length) {
    if (s1[i] === s2[j]) {
      i++
      j++
    }
    else {
      i = i - j + 1
      j = 0
    }
  }
  if (j >= s2.length)
    return i - s2.length
  else return -1
}

4.2.2. KMP 算法

例如，想要从 ababcabcacbab 中匹配 abcac，用暴力法就会出现下面的情况

索引	0	1	2	3	4	5	6	7	8	9	10	11	12
原串	$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ c }$	$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ c }$	$\displaystyle{ a }$	$\displaystyle{ c }$	$\displaystyle{ b }$	$\displaystyle{ a }$	$\displaystyle{ b }$
第 1 次	$\displaystyle{ a }$	$\displaystyle{ b }$	$\color{red}c$
第 2 次		$\color{red}a$
第 3 次			$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ c }$	$\displaystyle{ a }$	$\color{red}c$
第 4 次				${\color{red}a}$
第 5 次					${\color{red}a}$
第 6 次						$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ c }$	$\displaystyle{ a }$	$\displaystyle{ c }$

可以发现，这种情况下，效率就相对比较差。我们希望在副串移动时直接移动到合适的位置，并且 $\displaystyle{ i }$ 不应该回溯。

索引	0	1	2	3	4	5	6	7	8	9	10	11	12
原串	$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ c }$	$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ c }$	$\displaystyle{ a }$	$\displaystyle{ c }$	$\displaystyle{ b }$	$\displaystyle{ a }$	$\displaystyle{ b }$
第 1 次	$\displaystyle{ a }$	$\displaystyle{ b }$	$\color{red}c$
第 2 次			$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ c }$	$\displaystyle{ a }$	$\color{red}c$
第 3 次						$\color{gray}a$	$\displaystyle{ b }$	$\displaystyle{ c }$	$\displaystyle{ a }$	$\displaystyle{ c }$

右移位数 = 已匹配的字符数 - 对应部分的匹配值

Move = j - PM[j - 1]

使用部分匹配值时，每当匹配失败，就去找他前一个元素的部分匹配值，这样有些别扭，那就不妨把 PM 表右移一位，这样哪个元素匹配失败，直接看他自己的部分匹配值即可。

$\displaystyle{ a }$	$\displaystyle{ b }$	$\displaystyle{ c }$	$\displaystyle{ a }$	$\displaystyle{ c }$
-1	0	0	0	1

于是，上式改写成

Move = j - next[j]

相当于回退到

j = j - Move = j - (j - next[j]) = next[j]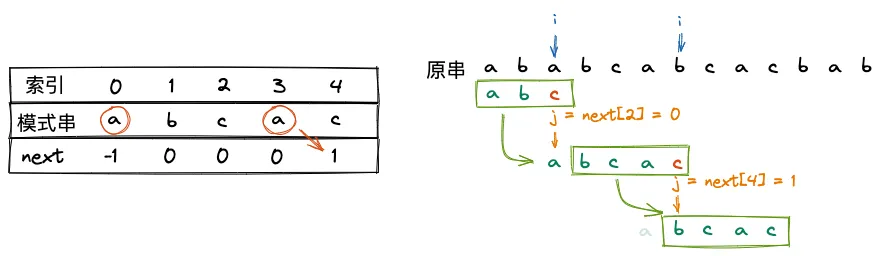

模式串与 next 数组

function getNext(t: string, next: number[]) {
  let i = 0
  let j = -1
  next[0] = -1
  while (i < t.length - 1) {
    if (j === -1 || t[i] === t[j]) {
      ++i
      ++j
      next[i] = j
    }
    else { j = next[j] }
  }
}

function kmp(s: string, t: string, next: number[]): number {
  let i = 0
  let j = 0
  while (i < s.length && j < t.length) {
    if (j === -1 || s[i] === t[j]) {
      ++i
      ++j
    }
    else { j = next[j] }
  }
  if (j >= t.length)
    return i - t.length
  else
    return -1
}

const t = 'abcac'
const next = Array(t.length).fill(0)

getNext(t, next)
const i = kmp('ababcabcacbab', t, next)
console.log(next, i)
// [-1, 0, 0, 0, 1] 5

4.2.3. KMP 算法的优化

next 数组在某些情况下仍然有一些缺陷，还可以进一步优化，例如 aaaab 与 aaabaaaab 的匹配

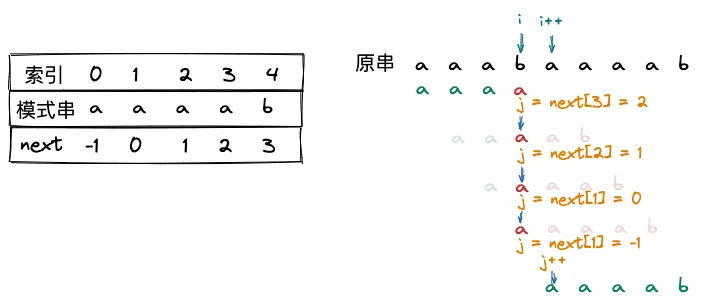
中间多了 3 次多余的匹配，因此我们可以考虑将它优化。

观察到，当 s[3] != p[3] 时，如果用 next 数组，还需要 s[3] 与 p[2], p[1], p[0] 分别匹配。

此时应当注意到，不应该出现 p[j] == p[next[j]]，因为当 p[j] != s[j] 时，下一次比较必然是 p[next[j]] 和 s[j]，因此需要 递归 一下，将 next[j] 修正为 next[next[j]]，直至两者不相等为止。

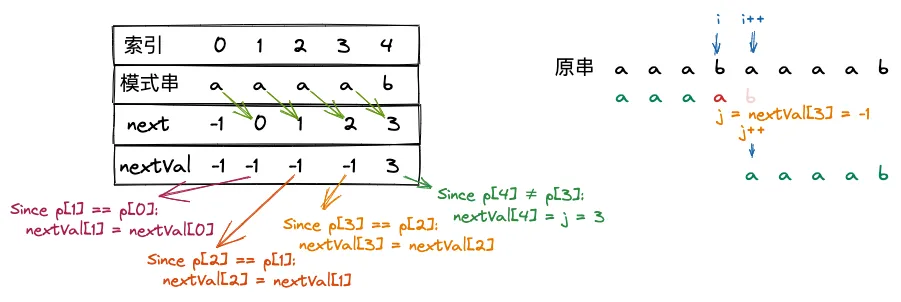
function getNextVal(t: string, nextVal: number[]) {
  let i = 0
  let j = -1
  nextVal[0] = -1
  while (i < t.length - 1) {
    if (j === -1 || t[i] === t[j]) {
      ++i
      ++j
      if (t[i] !== t[j])
        nextVal[i] = j
      else
        nextVal[i] = nextVal[j]
    }
    else { j = nextVal[j] }
  }
}

function kmp(s: string, t: string, next: number[]): number {
  let i = 0
  let j = -1
  while (i < s.length && j < t.length) {
    if (j === -1 || s[i] === t[j]) {
      ++i
      ++j
    }
    else { j = next[j] }
  }
  if (j >= t.length)
    return i - t.length
  else
    return -1
}

const t = 'aaaab'
const next = Array(t.length).fill(0)

getNextVal(t, next)
const i = kmp('aaabaaaab', t, next)
console.log(next, i)
// [-1, -1, -1, -1, 3] 4