Skip to content
Notes

概率论-数理统计

数理统计

总体 & 样本 & 统计量 & 样本数字特征

总体

数理统计中所研究对象的某项数量指标 X\displaystyle{ X } 的全体

样本

随机变量 X1,X2,⋯ ,XnX_{1},X_{2},\cdots, X_{n} 相互独立且与总体同分布，称 X1,X2,⋯ ,XnX_{1},X_{2},\cdots, X_{n} 为来自总体的简单随机样本

Tip
  • 样本均值 X‾=1n∑i=1nXi\displaystyle\overline{X}={1\over n} \sum\limits_{i=1}^{n}X_{i}
  • 样本方差 S2=1n−1∑i=1n(Xi−X‾)2\displaystyle S^{2}={1 \over n-1} \sum\limits_{i=1}^{n}(X_{i}-\overline{X})^{2}
  • 样本 k\displaystyle{ k } 阶原点矩 Ak=1n∑i=1nXik,k=1,2,A1=X‾\displaystyle A_{k}={1\over n} \sum\limits_{i=1}^{n}X_{i}^{k}, k=1,2, A_{1}=\overline{X}
  • 样本 k\displaystyle{ k } 阶中心矩 Bk=1n∑i=1n(Xi−X‾)k,k=1,2,B2=n−1nS2\displaystyle B_{k}={1 \over n} \sum\limits_{i=1}^{n}(X_{i}-\overline{X})^{k},k=1,2, B_{2}={n-1 \over n} S^{2}
性质
  • 如果总体 X\displaystyle{ X } 具有数学期望 E(X)=μE(X)=\mu，则 E(X‾)=μE(\overline{X})=\mu
  • 如果总体 X\displaystyle{ X } 具有方差 D(X)=σ2D(X)=\sigma^{2}，则 D(X‾)=σ2n,E(S2)=D(X)=σ2\displaystyle D(\overline{X})={\sigma^{2} \over n}, E(S^{2})=D(X)=\sigma^2
  • 如果总体 X\displaystyle{ X } 的 k\displaystyle{ k } 阶原点矩 E(Xk)=μk,k=1,2,⋯E(X^{k})=\mu_{k}, k=1,2,\cdots 存在，则当 n→∞n \to \infty 时，1n∑i=1nXik→Pμk,k=1,2,⋯\displaystyle {1\over n} \sum\limits_{i=1}^{n}X_{i}^{k} \xrightarrow{P} \mu_{k}, k=1,2,\cdots
证明
E∑i=1n(Xi−X‾)2=∑i=1n(EXi2−2EXiX‾+EX‾2)=∑i=1nEXi2−2X‾∑i=1nEXi+nEX‾2=∑i=1nEXi2−2X‾⋅nEX‾+nEX‾2=∑i=1nEXi2−nEX‾2\begin{aligned} E \sum_{i=1}^n \left(X_i - \overline{X} \right)^2 & = \sum_{i=1}^n \left( EX_i^2 - 2EX_i \overline{X} + E \overline{X}^2 \right) \\ & = \sum_{i=1}^n EX_i^2 - 2 \overline{X} \sum_{i=1}^n EX_i + nE \overline{X}^2 \\ & = \sum_{i=1}^n EX_i^2 - 2 \overline{X} \cdot n E \overline{X} + nE \overline{X}^2 \\ & = \sum_{i=1}^n EX_i^2 - nE \overline{X}^2 \end{aligned}

常用统计抽样分布

χ2\chi^{2} 分布

设随机变量 X1,X2,⋯ ,XnX_{1}, X_{2}, \cdots, X_{n} 相互独立且均服从标准正态分布 N(0,1)\displaystyle{ N \left( 0 , 1 \right) }，则称随机变量

χ2=X12+X22+⋯+Xn2\chi^{2}=X_{1}^{2}+X_{2}^{2}+\cdots + X_{n}^{2}

服从自由度为 n\displaystyle{ n } 的 χ2\chi^{2} 分布，记作 χ2∼χ2(n)\chi^{2}\sim \chi^{2}(n)

设 χ2∼χ2(n)\chi^{2}\sim\chi^2(n)
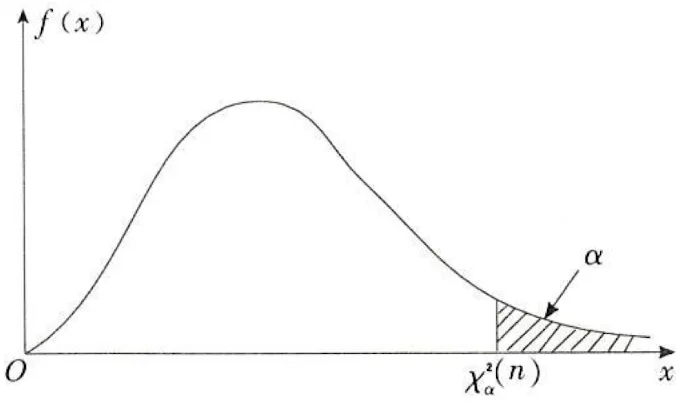
  • 对给定的 α(0<α<1)\alpha(0 < \alpha < 1)，称满足条件 P{χ2>χα2(n)}=∫χα2(n)+∞f(x)dx=αP\{\chi^{2}>\chi^{2}_{\alpha}(n)\}=\displaystyle\int_{\chi_{\alpha}^{2}(n)}^{+\infty}f(x) \mathrm{d} x=\alpha 的点 χα2(n)\chi_{\alpha}^{2}(n) 为 χ2(n)\chi^{2}(n) 分布上 α\alpha 分位点。对不同的 α\alpha 和 n\displaystyle{ n }，通常查表得到
  • E(χ2)=n,D(χ2)=2nE(\chi^{2})=n,D(\chi^{2})=2n
  • χ12∼χ2(n1),χ22∼χ2(n2)\chi_{1}^{2}\sim \chi^{2}(n_{1}), \chi_{2}^{2}\sim \chi^{2}(n_{2})，且 χ12\chi_{1}^{2} 和 χ22\chi_{2}^{2} 相互独立，则 χ12+χ22∼χ2(n1+n2)\chi_{1}^{2}+\chi_{2}^{2}\sim \chi^{2}(n_{1}+ n_{2})

t\displaystyle{ t } 分布

设随机变量 X\displaystyle{ X } 和 Y\displaystyle{ Y } 相互独立，X∼N(0,1),Y∼χ2(n)X \sim N(0,1),Y\sim\chi^{2}(n)，则称随机变量

T=XY/nT = {X \over \sqrt{Y/n} }

服从自由度为 n\displaystyle{ n } 的 t\displaystyle{ t } 分布，记作 T∼t(n)T\sim t(n)

性质
  • t\displaystyle{ t } 分布的概率密度函数是偶函数
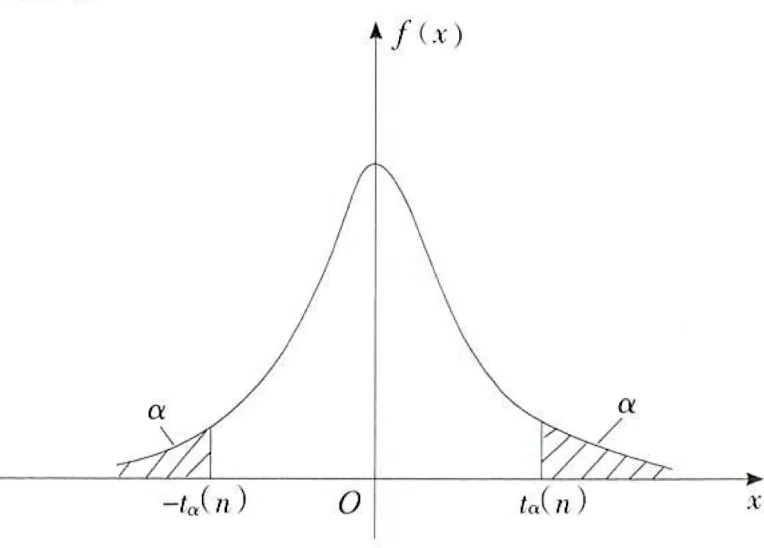
  • 设 T∼t(n)T\sim t(n)，对给定的 α(0<α<1)\alpha(0<\alpha < 1)，称满足条件 P{T>tα(n)}=∫tα(n)+∞f(x)dx=α\displaystyle P\{T > t_{\alpha}(n)\}=\int_{t_{\alpha}(n)}^{+\infty}f(x) \mathrm{d}x=\alpha 的点 tα(n)t_{\alpha}(n) 为 t\displaystyle{ t } 分布上 α\alpha 分位点
  • 由于概率密度为偶函数，可知 t\displaystyle{ t } 分布的双侧 α\alpha 分位点 tα/2(n)t_{\alpha/2}(n)，即 P{∣T∣>tα/2(n)}=αP\{|T|>t_{\alpha/2}(n) \}=\alpha，显然 t1−α(n)=−tα(n)t_{1-\alpha}(n)=-t_{\alpha}(n)

F\displaystyle{ F } 分布

设随机变量 X,Y\displaystyle{ X , Y } 相互独立，且 X∼χ2(n1),Y∼χ2(n2)X \sim \chi^{2}(n_{1}), Y\sim \chi^{2}(n_{2})，则称随机变量

F=X/n1Y/n2F={X/n_{1} \over Y/n_2 }

服从自由度为 (n1,n2)\displaystyle{ \left( n _{ 1 } , n _{ 2 } \right) } 的 F\displaystyle{ F } 分布，其中两个自由度分别称为第一自由度和第二自由度。

性质

对给定的 α(0<α<1)\alpha(0<\alpha<1)，称满足条件 P{F>Fα(n1,n2)}=∫Fα(n1,n2)+∞f(x)dx=αP\{ F > F_{\alpha}(n_{1},n_{2}) \}=\displaystyle\int_{F_{\alpha}(n_{1}, n_{2})}^{+\infty}f(x)\mathrm{d}x=\alpha 的点 Fα(n1,n2)F_{\alpha}(n_{1},n_{2}) 为 F(n1,n2)F(n_{1},n_{2}) 分布上的 α\alpha如果 F∼F(n1,n2)F\sim F(n_{1},n_{2})，则 1F∼F(n2,n1)\displaystyle{1\over F} \sim F(n_{2},n_{1})，且 F1−α(n1,n2)=1Fα(n2,n1)\displaystyle F_{1-\alpha}(n_{1},n_{2})={1\over F_{\alpha}(n_{2},n_{1})}

正态总体的抽样分布

一个正态总体

X∼N(μ,σ2),X1,X2,⋯ ,XnX \sim N(\mu, \sigma^{2}), X_{1},X_{2},\cdots,X_n 是来自总体的样本，样本均值为 X‾\overline{X}，样本方差为 S2S^{2}，则有

  • X‾∼N(μ,σ2n),U=X‾−μσ/n∼N(0,1)\displaystyle \overline{X}\sim N\left(\mu, {\sigma^{2}\over n}\right), U={\overline{X} - \mu \over \sigma /\sqrt{n} }\sim N(0,1)
  • X‾\overline{X} 和 S2S^{2} 相互独立，且 χ2=(n−1)S2σ2∼χ2(n−1)\displaystyle \chi^{2} = {(n-1)S^{2} \over \sigma^{2} } \sim \chi^{2}(n-1)
  • T=X‾−μS/n∼t(n−1)\displaystyle T={ \overline{X} -\mu \over S / \sqrt{n} }\sim t(n-1)
  • χ2=1σ2∑i=1n(Xi−μ)2∼χ2(n)\chi^{2}= \displaystyle{1 \over \sigma^{2} } \sum\limits_{i=1}^{n}(X_{i}-\mu)^{2}\sim \chi^{2}(n)

两个正态总体

X∼N(μ1,σ12),Y∼N(μ2,σ22)X \sim N(\mu_{1}, \sigma_{1}^{2}),Y\sim N(\mu_{2}, \sigma_{2}^{2})，Xi\displaystyle{ X _{ i } } 和 Yj\displaystyle{ Y _{ j } } 分别来自总体 X\displaystyle{ X } 和 Y\displaystyle{ Y } 且相互独立

  • X‾−Y‾∼N(μ1−μ2,σ12n1+σ22n2)\displaystyle\overline{X}-\overline{Y} \sim N\left( \mu_{1}-\mu_{2}, {\sigma_{1}^{2} \over n_{1} } + {\sigma_{2}^{2} \over n_{2} } \right)，U=(X‾−Y‾)−(μ1−μ2)σ12n1+σ22n2∼N(0,1)\displaystyle U={(\overline{X} - \overline{Y}) - (\mu_{1}-\mu_{2}) \over\sqrt{ {\sigma_{1}^{2} \over n_{1} } + {\sigma_{2}^{2} \over n_{2} } } } \sim N(0,1)
  • 如果 σ12=σ22\sigma_{1}^{2}=\sigma_{2}^{2}，则
T=(X‾−Y‾)−(μ1−μ2)Sω1n1+1n2,Sω2=(n1−1)S12+(n2−1)S22n1+n2−2T={(\overline{X} - \overline{Y}) - (\mu_{1}-\mu_{2}) \over S_{\omega} \sqrt{ { 1 \over n_{1} } + {1 \over n_{2} } } }, S_{\omega}^{2}={(n_{1}-1)S_{1}^{2} + (n_{2}-1)S_{2}^{2} \over n_{1}+n_{2}-2}
  • F=S12/σ12S22/σ22∼F(n1−1,n2−1)F=\displaystyle { S_{1}^{2} / \sigma_{1}^{2} \over S_{2}^{2}/ \sigma_{2}^{2} }\sim F(n_{1}-1,n_{2}-1)